1 января 2011
Освоение математики как путешествие, полное открытий
Согласно взглядам Л.С. Выготского, мышление для младенца означает ощущение (чувствование), для ребенка раннего возраста — восприятие, для дошкольника — вспоминание, а для школьника — умственную деятельность. Математика — это мышление. Таким образом, занятия математикой начинаются с младенческого возраста. На всех этапах психологического развития детям нужны адекватные поддерживающие программы, которые развивают ощущение, восприятие, память и собственно мышление.
Доктор философских наук Кристель Манске, создатель и директор Института развития функциональных систем мозга, вместе со своими коллегами работает с детьми, имеющими серьезные нарушения развития (ранний детский аутизм, синдром Дауна и др.). По ее мнению, основная проблема детей с трисомией-21 — не в органическом нарушении, а в отчуждении от общения с другими людьми. Она полагает, что развитие ребенка протекает успешно при следующих условиях:
1) если учитель и ученик отправляются в совместное путешествие с целью сделать открытие. Сожаление или отказ здесь абсолютно непродуктивны;
2) если учителю удается раскрыть ребенку его собственные возможности, донести до него, что ошибки естественны, а провала быть не может. Дети, как и взрослые, должны учиться на своих ошибках;
3) если мы понимаем, что термин «умственно отсталый» — это только выражение нашей неспособности использовать при обучении ребенка адекватные методы.
К. Манске – автор ряда книг, в том числе „Schlechte Schüler gibt es nicht“ – «Не бывает плохих учеников» (Basel, 1981), “Lernen können alle Leute” – «Учиться могут все люди» (Basel, 1990) и “Entwicklungsorientierter Lese- und Schreibunterricht für alle Kinder“ – «Обучение чтению и письму, ориентированное на всех детей» (Basel, 2004). Последняя по времени – книга “Jenseits von PISA. Lernen als Entdecklungsreise” – «По ту сторону PISA[1]. Учеба как путешествие, полное открытий» (Hamburg, 2008). Представляем вниманию читателей статью, основанную на материале одной из глав этой книги. В следующем выпуске нашего журнала мы планируем продолжить знакомство с этой книгой Кристель Манске.
Математика жизни
Математическое мышление нельзя сформировать путем подражания и уж точно невозможно – путем основательного заучивания. Это изумление, возникающее, когда удается приоткрыть завесу тайн, с которыми ребенок встречается каждый день. Если нет вопроса, никакой ответ не имеет смысла. В своем детстве я постоянно совершала физические и математические открытия.
Мне нравилось бросать в ведро с водой разные предметы – кусочки бумаги, дерева, камни – и наблюдать за тем, как они себя вели. Некоторые предметы уходили на дно, другие погружались и снова всплывали – одни быстрее, другие медленнее.
С понятием инвариантности мне помогла познакомиться овечья шерсть. Из целого мешка с шерстью получался маленький плотный клубок. В свои шесть лет я могла ответить на вопрос, что больше: мешок с шерстью или маленький клубок.
Уроки математики в школе были кошмаром. В гимназии все учителя говорили на немецком. Но с нашей речью их язык не имел ничего общего. Что хотел сказать учитель, когда он говорил об «удельном весе»?
Дедушка сходил в сарай и вернулся назад с куском дерева и куском железа: «Вот, смотри, возьми-ка их в руки, который из них тяжелей? У дерева свой удел, а у железа свой, они разные, поэтому у них разный удельный вес». Я сразу же его поняла.
Я боялась уроков математики почти до самого конца школы. Я не понимала ни интегралы, ни дифференциалы, ни тригонометрию. За три недели перед контрольной на аттестат зрелости одна профессор математики дала мне три бесплатных урока. Она принесла круглую вазу. «Вот, смотрите, самолет летит и делает дугу вокруг вазы?» Потом появилось то, что у нас называлось тригонометрией. Профессор держала нить в виде параболы над координатной системой, состоявшей из соломинок. Я все понимала без усилий и напряжения. Это было так просто, что на выпускной контрольной по математике, держа в голове только нитку, круглую вазу и координатную систему, состоящую из трех соломинок, я смогла правильно составить уравнения и сделать рисунки. Как же это оказалось возможным, что за несколько часов я поняла больше, чем за два последних года своего обучения математике? Когда речь идет о мышлении, о внутреннем плане действий, использование наглядного материала становится очень важным. Предпосылкой совместно разделенных значений является совместно разделенный смысл.
Математика оказывается важнейшим вопросом для жизни. Ральф работал в мастерской для умственно отсталых, и все считали, что «вычислительный центр» в его голове попросту отсутствует. Он был исключен из учебного процесса для нормальных детей из-за своего необычного способа видения вещей. Он сдал бы экзамен на аттестат зрелости, если бы встретил хотя бы одного учителя, который смог бы воспринимать вещи так же, как он.
Когда Тимо пришел ко мне на занятия, ему было 10 лет. Он посещал школу для детей, нуждающихся в психологической поддержке. Он не справлялся с простыми заданиями, где нужно было оперировать числами в пределах десятка. За полгода Тимо наверстал четыре года, которые он потерял в школе. Сейчас он учится в элитной гимназии в Англии и благодаря своим удивительным дарованиям получает особую стипендию. Тимо хочет учиться в Гарвардском университете и собирается написать книгу под названием «С IQ 83 в Гарвард».
Инвариантность, реверсия, классификация, сериация, равенство и неравенство – всё это открытия, которые должен сделать для себя каждый ребенок, общаясь с другими людьми. Совместно разделенное значение не существует без совместно разделенного смысла.
А вот история, которую рассказал Ральф: «Шнукки съел булочки». Учительница нарисовала на доске шесть кружочков (булочек), потом минус, потом еще четыре кружочка, а потом знак «равно». Затем учительница перечеркнула четыре кружочка, а два оставила целыми и сказала, что шесть минус четыре равняется двум.
Для Ральфа перечеркивание кружочков вовсе не означало, что Шнукки съел эти булочки. Для него это означало деление пополам. Но учительница – без предупреждения – с символического уровня (где кружочки символизировали булочки) перешла в систему знаков. Теперь для нее (в системе знаков) перечеркивание кружочка означало, что собака съела булочку, а для Ральфа, который остался в системе символов, это означало, что булочка была разделена пополам. Не удивительно, что Ральф сказал: «Мне что-то ничего не понятно».
При исследовании развития логического мышления у детей с трисомией-21 мы встречаемся с серьезными трудностями. У таких детей ни в школе, ни дома, как правило, нет занятий математикой. До школы, когда должны образовываться все нейронные связи, также обычно не происходит ничего такого, что имеет отношение к формированию логического мышления, кроме разве что «посчитай один – два – три».
В настоящее время основные цели нашей работы состоят в том, чтобы обратить внимание родителей и учителей, воспитателей и врачей на таких детей, сделать так, чтобы они увидели их потенциал и осознанно приняли то различие, которое существует между ними и обычными детьми. Необходимы научно обоснованные занятия для этих детей, находящихся на различных возрастно-психологических уровнях (для маленьких детей, дошкольников, школьников). Анализ таких занятий позволил бы постепенно совершенствовать их. Проведение семинаров и издание соответствующей литературы способствовало бы лучшему пониманию сущности когнитивного развития вообще и математического мышления в частности. Речь идет не о готовых рецептах проведения занятий, а о теоретических и практических исследованиях, позволяющих подбирать соответствующие подходы для обучения самых разных детей.
С каждым ребенком мы занимаемся 45 минут в неделю. В год получается – за вычетом каникул и пропусков по болезни в среднем 27 часов. Если мы сравним эти немногочисленные часы с теми достижениям, которых добиваются дети в ходе этих занятий, то перед нами неизбежно встанет вопрос: «Чего же можно было бы достичь, если бы с детьми ежедневно в течение двух – пяти часов занимались обученные специалисты?»
Пока мы ищем истоки проблемы обучения математике детей с трисомией-21 в самих детях, мы никогда не разрешим эту проблему. Как учителя мы должны задуматься о том, что считаем этих детей неспособными к мышлению еще до того, как начинаем с ними работать. Мы должны сделать все возможное, чтобы перестать исключать их из процесса обучения математическому мышлению. Мышление, сознание – невидимые процессы. Нам пока непонятны эти процессы у детей с трисомией-21. Дети же воспринимают наше непонимание как помеху, как неправильное поведение, от которого они защищаются всеми возможными средствами. Отвлечение, отказ, агрессия, разочарование – всё это защитные стратегии, предполагающие наличие интеллекта. Как мы можем узнать у детей, в чем состоят тенденции их развития, какая помощь им нужна? Они не могут учиться у нас, пока мы не начнем учиться у них. Если мы терпим неудачи, мы должны подключить интуицию и любопытство, как следует сосредоточиться и не торопиться, только тогда у нас смогут возникнуть адекватные педагогические идеи.
В основе математического мышления лежат функциональные системы, которые не являются врожденными, а складываются постепенно – сначала в поле восприятия, в ходе совместно разделенной деятельности с разнообразными предметами, затем на уровне символических действий с использованием фотографий и пиктограмм и с формированием воспоминаний и, наконец, на уровне знаков с формированием умственных действий. Как только мы согласимся, что в основе математического мышления лежат функциональные системы мозга, которые перестраиваются на разных возрастно-психологических этапах развития ребенка, мы придем к выводу, что ни один ребенок не рождается с готовым «вычислительным центром» в голове. Наличие или отсутствие такого «центра» не является биологическим фактом, это процесс социального становления, который во многом является отражением адекватного или неадекватного способа преподавания.
Способность к формированию математического мышления – биопсихосоциальный процесс. В истории человечества развитие «вычислительного центра» нашего мозга происходило благодаря употреблению различных инструментов – от орудий ручного труда до внутренних, психологических инструментов, т. е. от создания каменного топора неандертальцем до развития теории относительности Эйнштейном. В ходе онтогенеза также необходимо предоставлять детям возможности для овладения различными инструментами.
Математическое мышление не начинается с простого счета, поскольку, когда мы говорим «единица», у нас уже есть повод задуматься. То, что для одних является единицей, для других оказывается двойкой. Если я разрезаю яблоко пополам, получается две половинки. Если я говорю, что одно большое яблоко равно двум маленьким, то единицей становится половинка большого яблока. Все это невозможно объяснить детям с помощью слов. Детям нужен разнообразный опыт для того, чтобы они смогли включить понятие числа «один» в целостную систему количественных измерений.
Математика – это восприятие и память
Классификация
Для формирования понятия числа необходимо, чтобы были сформированы операции классификации и сериации.
Уже в возрасте от одного года до трех дети способны классифицировать предметы по цвету: «Все красные мячики нужно сложить в красную корзинку, а все синие – в синюю». То же самое они могут делать с кубиками, фигурками LEGO и т. д. Таким образом, дети в самом раннем возрасте узнают четыре основных цвета и могут обозначать их с помощью речи или жестов. Затем дети учатся сортировать предметы по двум категориям – цвету и форме, например используя разноцветную пластиковую посуду: «Сложи все красные приборы в отдельную коробку, затем все синие, затем зеленые, затем желтые. А теперь сложи все вилки, потом все ложки, потом все ножи». Уже в три года детям известны понятия «цвет» и «форма». Затем они начинают замечать, что одинаковое все же различно. Ганс говорит: «Эта вилка не такая красная, как та». Всё зависит от критериев, на основе которых принимается решение о том, что относится к данной категории, а что нет.
Достигнув дошкольного возраста, ребенок учится логическому мышлению: начинает складывать по цвету, форме и размеру треугольники, кружки, прямоугольники и квадраты. Он учится обозначать геометрические понятия. Начиная с четвертого года жизни ребенок учится идти наперекор своему восприятию. Он начинает подводить под одно понятие совершенно разные предметы. Например, он понимает, что «средство передвижения» это машины, лодки, самолеты, велосипеды, автобусы и ракеты, которые могут быть сделаны из дерева, металла или картона.
Затем ребенок учится подбирать к предметам карточки с их изображениями. Жозефина (4 года, трисомия-21) подкладывала карточки с изображениями к игрушкам, разложенным по видам. В конце у нее осталась карточка, на которой была изображена зебра. «Зебры нет, нет зебры!» – огорчилась она. Затем посмотрела на цветы в вазе, машины на парковке, мебель в кукольном доме и, сказав: «Зебра – это тоже зверь!», положила карточку с изображением зебры к остальным животным. Жозефина открыла для себя метод индукции.
Категория величины, в том виде, в котором она встречается в логических блоках, является не свойством объекта, а способом сравнения. Господин Хайнрих принес три плитки шоколада разного размера. Он положил маленькую плитку рядом со средней: «Марвин, какая плитка больше?» Марвин показал на среднюю. Затем господин Хайнрих положил среднюю плитку рядом с большой: «А теперь?» Марвин опять показывает на среднюю и ухмыляется: «Эта больше. Ты же сам сказал!»
Сериация
Когда я познакомилась с Арно, ему было уже больше двадцати. Я положила на стол конфеты: «Здесь три конфеты: один, два, три». Юноша взял конфеты и разложил их по-новому – сначала третью, потом остальные две. «Три, два, один!» – сказал он с сияющим лицом. Я сказала ему, что числа всегда идут по порядку, у каждого числа – свое место. Число 4 всегда располагается между числом 3 и 5. Он вопросительно смотрел на меня: «Разве это хорошо? Четверка должна хоть раз побывать на месте единицы». Прежде чем начать считать с детьми, мы должны в совместно-разделенной деятельности открыть с ними понятие числа, точно так же, как это происходило в истории человечества.
У Алины тоже было свое представление о сериации. Расставляя матрешек, она сказала мне: «Маленькую нужно поставить вот сюда, между мамочкой и папочкой!» Но когда я расставила их по порядку и объяснила, что это стадии роста ребенка, Алина радостно воскликнула: «Я знаю! Я знаю! Ребенок становится больше!»
В соответствии с принципом сериации дети складывают из кубиков лестницу, из колец пирамидку, из ведерок башню. При этом каждая ступень в лестнице, этаж в пирамидке или в башне имеет свое место, как и число на числовой прямой.
Инвариантность
Любое открытие таит в себе волшебство. Максу нравилось играть в фишки. Фишки были двух видов: одни более тонкие, из металла, вторые потолще, из пластика. Я сложила все фишки в две стопки и спросила Макса: «Каких фишек у тебя больше?» Он поставил обе стопки рядом, чтобы сравнить, и ответил: «Пластиковых».
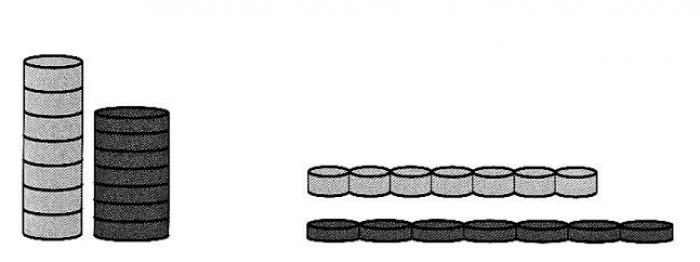
Затем я выложила все фишки в два ряда. Мальчик замер: «Как же так? Сначала пластиковых фишек было больше, а потом вдруг – металлических». Макс всю неделю задавал себе этот вопрос, не находя ответа. Он не знал, что есть такие понятия, как радиус и высота. Как только он сделал это открытие, неизвестное вдруг стало простым и понятным. Но если нет вопроса, любой ответ становится бессмысленным.
Жозефина высыпала четыре ведерка песка в высокий сосуд и столько же в плоскую миску. Высыпая ведерко песка, Жозефина наклеивала на емкость синий листочек бумаги. Учительница спросила ее: «Где больше песка?» Жозефина показывает на высокий сосуд: «Смотри, тут больше, да?» Затем она показывает на миску и добавляет: «А здесь, смотри, здесь ведь меньше или…» Волнуясь, она как бы перебивает саму себя: «Но ведь и здесь и там – одинаково!» Память в этом случае побеждает восприятие. Выготский пишет, что на возрастно-психологическом этапе дошкольника ребенок вспоминает, когда думает, а на возрастно-психологическом этапе школьника, напротив, ребенок думает, когда вспоминает. На этом этапе происходит психическая реструктуризация. У дошкольников память все еще является доминантой, ведущей деятельностью. На этой основе у них и развивается мышление. Поэтому урок математики всегда должен соответствовать актуальной структуре психики ребенка.
Количественный счет
Дети, которые еще не умеют представлять в уме количество каких-либо предметов, сначала разнообразными способами учатся символизировать его. Например, они лепят шарики из пластилина, завязывают узелки, рисуют картинки. На своих занятиях я всегда говорю детям: «Закройте глаза и вспомните о том, что вы делали, или вспомните картинки, которые вы только что нарисовали». Только так у детей появляется возможность построить внутреннее событийное пространство, научиться производить умственные операции. Для дошкольника математика строится на процессе вспоминания. Занятия с наглядным материалом, которые обычно проводятся с маленькими детьми, лишь фиксируют их на этой стадии, не помогая им перейти на стадию символического рисунка.
Для того чтобы у детей сформировалось понятие множества, у них должна быть возможность отвлечься от качества предметов и сосредоточиться только на их количестве. Для этого мы, например, использовали картинки с изображением самых разных предметов, а рисование штрихов помогало детям абстрагироваться от качеств этих предметов.
Мне стало понятно, насколько это важно, когда я сказала одному из родителей: «Ребенок, который все еще находится на стадии восприятия, не может представить себе, что 5 мышей больше, чем 2 слона». Его сынишка, стоявший рядом, добавил: «Ну вот, папа, теперь ты знаешь, что 2 слона все-таки больше».
Математика – это мышление
Сложение
Однажды Ральф сказал мне, что ему неинтересно сложение, поскольку оно означает, что люди жадные и хотят иметь все больше и больше. Когда он познакомился со знаком равенства в примере 3+4=7, математика приобрела для него совершенно иной смысл. Теперь он воспринимал знак равенства как инструмент для «установления справедливости», когда два человека имеют право на одинаковое количество. Поэтому и задание по заполнению пропуска, например, «3+…=7», не вызвало у него затруднений. Ральф не считал по одному, как это часто бывает у детей, имеющих проблемы со счетом. Он рассуждал вслух: «Тот, у которого 3, получил меньше.Родители должны дать ему еще 4». Анника решает пример 3+4=?, используя символы, а затем записывает его цифрами. Анника поясняет: «Я читаю: 3. Рисую  , потом читаю +, это значит прибавить. Потом читаю 4. Рисую
, потом читаю +, это значит прибавить. Потом читаю 4. Рисую 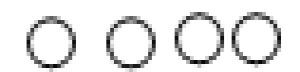 , считаю: 7».
, считаю: 7».
Вычитание
Анника обожает вычитать. Госпожа Нойман кладет 5 конфеток на стол. Задание заключается в решении примера 5–2=?
Анника забирает две конфетки и говорит: «Осталось три!» Она может съесть те конфетки, которые взяла. Так как девочка не может бесконечно кушать сладости, госпожа Нойман придумывает игру со свинкой-копилкой: «Хрюшке дают 5 конфеток. Две из них она съедает сразу». Анника кидает две конфетки в копилку. Вскоре Анника уже может работать с символической, т. е. нарисованной копилкой. Это доставляет ей такое удовольствие, что теперь решение примера становится для нее важнее, чем возможность есть сладости. Роль ученицы помогает формированию ее самосознания.
Единство реального и символического действия является предпосылкой к тому, чтобы выявлять смысл и значение при работе на символическом уровне.
Позиционная система исчисления
Числа не интересовали Матти. Поскольку ему очень нравились полудрагоценные камни, мы попытались научить мальчика считать хотя бы их. Он умирал со смеху, когда я вслух считала камни – от 1 до 10.
Когда ему было десять лет, он нашел в супермаркете один пфенниг. Два месяца спустя он насобирал целую коллекцию разных монет. Его сестра тем временем случайно нашла на улице купюру в пять марок. «Что больше, пять марок или все мои деньги?» – спросил Матти. Я разложила его монеты в стопки по 10 пфеннигов так, что он увидел, как из единиц получаются десятки, а из десятков – сотни, и тут же все понял. Здесь не было счета от единицы до бесконечности, здесь была система. Матти почти с разочарованием спросил меня: «Госпожа Манске, почему Вы раньше от меня это скрывали?» Он стал специалистом по торговле в розничной сети. В его свидетельстве о повышении квалификации в графе «экономические расчеты» стоит отметка «очень хорошо».
У Марвина трисомия-21. Когда я стала заниматься с Марвином счетом с использованием позиционной системы счисления, я положила три красных кружочка под разрядом десятков и два синих – под разрядом единиц: «Считай». Марвин ответил: «Пять. Моя учительница говорит, что три красных плюс два синих кружка будет пять. А ты говоришь, что один красный означает десяток, а один синий – единицу. Тогда получается 32». Мальчик хитро смотрит исподлобья. Он хочет донести до меня смысл своих слов: «Мне нужно считать двумя разными способами». К счастью, после разговора со мной его учительница математики тоже начала использовать позиционную систему исчисления.
Переход к десяткам
Кристоф – ребенок, нуждающийся в интеграции. Мальчик легко справлялся с такими примерами, как 7 – 5 = , 8 + 9 = , 35 – 8 = , если пользовался специальной доской, расчерченной на сто квадратов, а затем записывал решение в свою тетрадь. Он мог считать только по одному. Ему нравилось заниматься математикой, но никакого продвижения в его развитии не наблюдалось. Он успешно справлялся с действиями в поле восприятия. Но удерживать в уме цифры, понимая, что они означают количество, и проводить с ними математические операции он не мог.
Совместно-разделенный смысл должен быть основой любого занятия, иначе оно бесполезно как для ученика, так и для учителя. Этот смысл открывается нам тогда, когда мы наблюдаем за действиями детей, ведь мы всегда должны понимать, что ребенок делает что-то, исходя из собственного смысла. Когда А. Н. Леонтьев увидел, что дети считают 3 + 4 = 7 на пальцах, он не стал запрещать им делать этого, а спросил, по какой причине они так поступают. Он обратил внимание также на тех детей, которые повторяли задание вслух, и на тех, кто думал, приложив указательный палец к виску.
Леонтьев наблюдал за процессом развития у детей математических способностей, начиная со счета на пальцах, через громкую речь и заканчивая счетом в уме.
«Я обратил внимание, – пишет А. Н. Леонтьев, – на то, что ученики, складывая в уме числа, скрыто пользуются при этом пальцами. Тогда я попросил принести несколько блюдец, дал по два блюдца каждому ученику и предложил им приподнимать их над столом в то время, когда они будут отвечать. Оказалось, что при этих условиях операция сложения чисел у большинства из них полностью распалась. Более подробный анализ показал, что в сложении эти ученики фактически остались на этапе внешних операций "присчитывания по единице" и переход к дальнейшему этапу у них не произошел. Поэтому продвинуться в обучении арифметике дальше действий в пределах первого десятка без специальной помощи они не могли. Для этого нужно было не вести их дальше, а, наоборот, прежде возвратить их к первоначальному этапу развернутых внешних операций, правильно "свернуть" эти операции и перевести их в речевой план – словом, заново построить у них способность “считать в уме”.
Как показывают исследования, подобная перестройка действительно удается даже в работе с детьми с достаточно резко выраженной умственной отсталостью. Особенно же важно, что в случаях небольшой задержки умственного развития это дает эффект полного устранения ее.
Конечно, такое вмешательство в процесс формирования тех или иных умственных операций должно быть своевременным, потому что в противном случае из-за иногда случайно не сложившегося или неправильно сложившегося этапа формирования данного процесса он не может далее нормально протекать, в результате чего и создается впечатление о якобы умственной неполноценности данного ребенка»[2]
Эти слова стали для меня поводом к полной реструктуризации процесса обучения с разделением его на три этапа: действие – громкая речь – «тихое» мышление. Затем я добавила еще одну ступень между действием и громкой речью – этап символики. Таким образом, процесс обучения начал соответствовать этапам развития в онтогенезе. Если строить занятия по этой схеме, то все дети смогут участвовать в обучении, поскольку в процессе их актуального развития будут учтены все возрастно-психологические этапы онтогенеза.
Так я пришла к тому, чтобы спровоцировать Кристофа к символическому действию. «Ты можешь построить из восьми клеток своей тетради какой-нибудь предмет?» Мальчик без труда нарисовал цветную подводную лодку. Для этого ему понадобились четыре оранжевых и четыре синих клетки. Я попросила его по памяти построить эту лодку из пластмассовых кубиков. Он без труда все вспомнил: «У меня было четыре синих кубика, к ним я прикрепил три оранжевых, и потом еще один оранжевый». Он закрыл глаза, наморщил лоб и начал считать: 4+3+1=8. Я впервые увидела, как он думает, как выходит из поля восприятия. На последующих занятиях он еще несколько недель играл с кубиками – строил из них животных, машины, мебель, дома. Я просила его по памяти зарисовывать все эти объекты в тетрадь по математике. И он ни разу не ошибся. Затем я предложила ему: «А теперь представь, что у тебя на столе с одной стороны лежат восемь синих кубиков, а с другой – четыре красных». Мальчик рисует у себя в тетради заданный пример. «Я знаю, сколько будет восемь плюс четыре. Двенадцать!» Сейчас Кристоф в уме составляет задачи на сложение с помощью своей счетной доски. «Кладу 18 синих кубиков на доску. Округляю до 20 – делю красную четверку на две двойки. Теперь у меня два полных десятка и еще двойка. В итоге получается 22». Как произошла эта реструктуризация в его мозге, я не знаю. Мне известно только то, что процесс начался с взаимодействия с предметами в поле восприятия и с помощью символического действия (рисования в тетради) перешел к возникновению внутренних образов в уме. Только после этого использование знаков и цифр приобрело для него смысл.
Умножение
Господин Хайнрих рассказывает о том, как он хотел научить Марвина умножению: «Когда я начал выкладывать на стол связанные в пучки счетные палочки, он сказал: ”Мне нужен картон, пластилин и деревянные палочки, чтобы построить Чертов Котел” – и начал втыкать палочки в фундамент из пластилина. Он действовал, как будто у него был заранее подготовленный план. Получалось, что руководил занятием он, а не я. На последующих трех занятиях мы построили под руководством Марвина форт, хижину на деревьях и скалу. Как только я начинал строить что-либо самостоятельно, он тут же поправлял меня, добиваясь того, чтобы мои действия совпали с его внутренними представлениями. Марвину было нетрудно мне противоречить. Он не ожидал от меня похвалы. Гораздо важнее для него было совместное достижение поставленной цели. А для меня главным было то, что он воплощает свои внутренние тенденции в действия и может о них рассказывать. Когда наш Чертов Котел и все строения внутри него были готовы, мы начали проводить с их помощью разнообразные математические операции, такие как обмер поверхностей, сравнение количества предметов и т. п. К моему удивлению, Марвин решил пример 4 х 2 = 8 без предварительных упражнений по умножению. Тогда я вспомнил слова Леонтьева о том, что функциональные системы, когда они формируются на основе единства действий и речи, способны к трансформации и генерализации. В отличие от механически заученного материала, например заученной в школе таблицы умножения, функциональные системы являются очень устойчивыми и защищены от стирания. Математическое мышление формируется в единстве опыта, символики, в которой выражается этот опыт, обозначения и схематизации. Главное в нашей работе – это позволять проявляться присущим ребенку тенденциям и соответствовать им в своих действиях.
Деление
Для школьника думать – значит приводить свои действия в соответствие с реальностью. Ральфу математика казалась пустой тратой времени, потому что она не была направлена на восстановление справедливости.
«8 : 4=2 – это деление. Сначала мы посчитаем этот пример с помощью кукол и монет, а потом запишем его на бумаге». Я поставила на стол четыре куклы и разделила монеты между ними не поровну. Я наделась, что Ральф скажет, что монеты распределены неправильно. Но мальчик сказал, нисколько не помедлив: «Я получаю одну марку в час. Я и есть та кукла, которая получила одну марку. Первая кукла, я думаю, это начальник, вторая – мастер, а четвертая не получила ничего». Я потеряла дар речи. После долгого молчания я все же спросила: «Как бы ты разделил эти восемь монет между четырьмя куклами?» Ральф ответил: «Я не могу бороться за свои права. Это могут сделать только опытные, уверенные в себе люди. Обычно все деньги достаются начальнику. Но ведь это же несправедливо». Тогда я разделила восемь монет поровну и дала каждой кукле по две. Ральф подпрыгнул на месте и радостно воскликнул: «Почему Вы раньше не сказали? Вы разве не знаете, что для меня главное – это равенство? Значит, так же можно посчитать 24 : 8 и 15 : 5? Я знал, что получится 2, но не знал, почему. В школе всегда говорили, что 8 разделить на 2 будет 4, потому что 2 умножить на 4 – это 8, но никогда не объясняли, почему это так. И никогда не говорили, что нужно обращать внимание на знак равенства».
Текстовые задачи
«Госпожа Шмидт дала Карине 10 марок и отправила ее за покупками. Ей нужно потратить 6 марок в булочной и 3 марки в продуктовом магазине». Когда я читала детям условие задачи вслух, они запоминали отдельные слова, не вкладывая в них никакого смысла, например «в булочной – шесть». Как только я попыталась разыграть с ними сценку с участием персонажей задачи, дети сразу узнали в ней повседневную ситуацию, когда родители просят их купить что-то в булочной, например булочки или пирог. Только тогда, когда дети могут поместить задачу в контекст собственного опыта, они в состоянии использовать свои ресурсы для ее решения, их потенциальные возможности становятся основой для формирования функциональных мозговых систем. Мы предложили Жозефине (12 лет) представленный в виде комикса вариант того же самого задания. Она без труда смогла пересказать, проиграть и решить эту задачу. Решать текстовые задачи в картинках – одно удовольствие!
Путь поиска решения
В нашей работе не бывает неудач. Потому что нам неважно, правильно ли ребенок решил задачу, для нас важен путь, по которому ребенок идет к знанию. Если он говорит нам, что трижды пять – шестнадцать, и при этом объясняет, что он перемножил 3 связки счетных палочек, в каждой из которой было 5 штук, то такой ответ нас вполне устраивает и считается верным. Нам становится ясно, что ребенку понятен механизм счета. Мы даем ему возможность самому проверить свои результаты и исправить ошибку. Если же ребенок дает нам сразу правильный ответ и поясняет, что просто выучил наизусть таблицу умножения, мы понимаем, что он заблуждается. На вопрос «Сколько будет 5 х 11?» он отвечает: «Так не бывает». А тот, что ошибся в первом примере, наоборот, улыбнется и скажет: «5 х 10 будет 50 и еще пятерка!»
Учитель всегда рад, когда ученик ищет ответ. Открытия происходят сами, когда есть возможность действовать. Урок математики – это путешествие, полное открытий.
[1] PISA (Program for International Student Assessment) – Международная программа по оценке образовательных достижений учащихся.
[2] Леонтьев А. Н. Принципы психического развития ребенка и проблема умственной недостаточности // Леонтьев А. Н. Проблемы развития психики. 4-е изд. М. : Изд-во Моск. ун-та, 1981. С. 555–556].
Автор:
Благотворительный фонд «Даунсайд Ап» / Манске Кристель
Возраст до:
12
Возраст от:
6
Источник:
Журнал «Синдром Дауна. XXI век», № 1 (6)
Категория:
Специалистам
Правообладатель:
Благотворительный фонд «Даунсайд Ап»
Тип материала:
Статьи
Теги материала:
навык / методика обучения / трудности / обучение математике
Количество показов:
13449